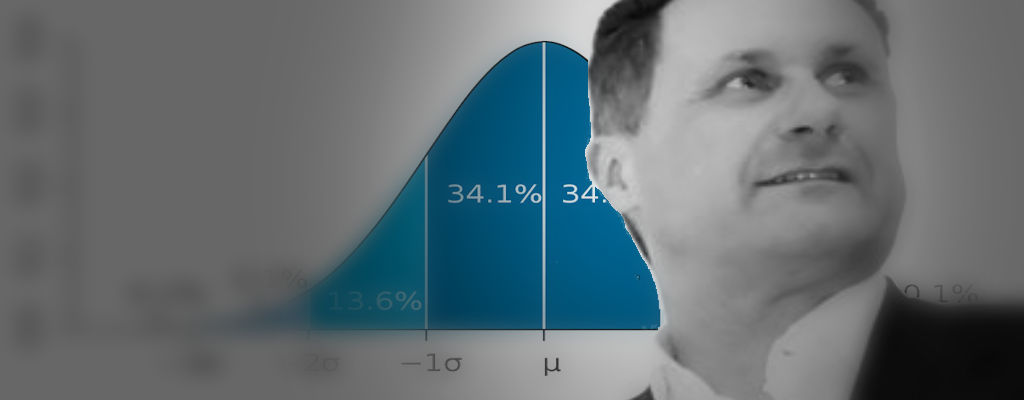
Quando il tuo consulente qualità non sa la matematica

Quando sento gli imprenditori parlare male dei sistemi qualità, e dei consulenti relativi, mi metto la mano sulla coscienza e cerco di vedere i problemi dal loro punto di vista.

Poi mi ricordo che anche io sono un imprenditore (alla consulenza dedico sempre meno tempo, ho diverse altre mie attività da mandare avanti) e mi rendo conto dell’inutilità di certe tecniche spacciate per strumenti della qualità, o meglio, come tutte queste tecniche vengano elargite alle PMI con il copia e incolla, senza minimamente sapere quali basi matematiche le supportino.

Detta così sembra complicato, ma se ti faccio dei casi pratici ti rendi immediatamente conto di quello che parlo:

nei tuoi processi produttivi, quanti pezzi controlli e ogni quanto? Perchè fai così?

quando ricevi del materiale in ingresso dai fornitori, quanti pezzi controlli? Perchè fai così?

Se la risposta alle domande è diversa da “Perché ho fatto dei calcoli”, sei fuori strada e chi ti ha suggerito quel metodo non aveva le corrette (e minime visto l’argomento) basi matematiche e statistiche.

Ma devo sapere la statistica?

Intanto spieghiamo una cosa importante: perché si usano tecniche statistiche per fare i controlli?

Semplice, perché le tecniche statistiche ti permettono di stabilire se il tuo lotto di pezzi (di produzione o in ingresso) sia conformi o no, controllando un numero limitato di pezzi (campione).

Quindi, se hai lotti molto numerosi, controllandone un numero ridotto sai se puoi spedire o accettare il lotto: un bel risparmio di tempo, ma che puoi ottenere solo se sai esattamente cosa fai in termini matematici.

Intanto consideriamo che le tecniche statistiche si possono applicare solo se il numero di pezzi prodotti, e da controllare, è elevato, quindi se fai produzioni di pochi pezzi questo articolo sarà solo accademico, ma poco pratico.

Per tutti gli altri serve conoscere un po’ di statistica ed è importante imparare ad applicarla nel modo migliore possibili.

Le tecniche preconfezionate

Il controllo statistico del processo (SPC) è fatto anche attraverso l’uso di tecniche che sono state studiate per agevolare il compito agli operatori fornendo strumenti visuali efficaci (per esempio le carte di controllo). In questo caso è sufficiente conoscere come usare questi strumenti, non necessariamente la base matematica che sta dietro.

E’ inoltre possibile dedurre i piani di campionamento da apposite norme UNI che, partendo dal livello qualità accettabile, ed in funzione di parametri quali la numerosità del lotto e la severità del controllo, determinano quanti pezzi controllare: bellissimo, ma cosa ci sta dietro?

E’ chiaro che questo articolo non pretende di insegnare la statistica a nessuno, farò giusto qualche accenno che ritengo utile, ma voglio sottolineare il fatto che le aziende che non conoscono le tecniche statistiche e fatto i controlli campionando a caso, o a sensazione, hanno un sacco di scarti e di clienti arrabbiati.

Ma a questo punto ti chiedo: chi ti ha insegnato a lavorare così?

Ok, i consulenti, lo sapevo, quelli che l’azienda voleva pagare poco o niente perché tanto la ISO 9000 è solo una seccatura.

Un problema dei Responsabili Qualità sono i clienti ignoranti (e arroganti)

Se lavori con aziende che hanno clienti strutturati sai che periodicamente ti becchi gli audit dei clienti e che spesso l’audit entra nello specifico dei controlli che fai in produzione.

Purtroppo capita spesso che il cliente ti abbia fatto delle richieste illogiche già in fase di sviluppo prodotto e tu (la tua azienda), non avendo basi matematiche, le hai accettate senza fiatare. Quando poi sei andato in produzione ti sei accorto che non aveva senso fare certi controlli con determinate frequenze e modalità, e hai quindi deliberatamente scelto di non farli come previsto. A quel punto iniziano le discussioni con il cliente che, quasi sempre, usa il suo potere di cliente per “convincerti”, ma, quasi mai, ha degli argomenti scientifici da mettere sul tavolo.

Perchè dovrei fare un controllo di 2 pezzi una volta all’ora quando ho un tasso di errore del 10%?

Perché faccio un controllo visivo al 100% su caratteristiche estetiche, sapendo che il cliente accetta 0 (zero) errori su 1.000.000 di pezzi e il tuo controllo visivo lascia passare il 5%?

Quale è la logica per cui fai tutto ciò?

Semplice, che non ti hanno insegnato cosa sia la statistica.

Giusto per interessarti un po’

La statistica studia la probabilità che si verifichi un evento: non esistono eventi certi in statistica, ma solo più o meno probabili.

Quindi, in statistica non c’è niente di certo, semmai molto probabile o molto improbabile, e quindi ogni calcolo statistico comporta un possibile errore (quindi bisogna “stare larghi” per essere sicuri).

Chi di voi si è sentito chiedere il CPk, la capacità di processo di processo e si è sentito dire che il valore minimo non doveva essere inferiore a 1,33 (o latri valori specificati dal cliente)?

Perché 1,33?

Semplice: in ultima analisi (semplificando un po’) la capacità macchina e di processo sono la capacità del mio processo o macchina di “stare nelle tolleranze”. Sono il rapporto tra campo di tolleranza e distribuzione delle misure (poi ti spiego cosa è la distribuzione) e quindi 1 potrebbe andare bene, ma siccome bisogna “stare larghi” per compensare l’errore statistico il cliente chiede 1,33.

Capito di cosa parliamo?

Immagina di dover tagliare 10.000 tubi di metallo della lunghezza di 100 mm con tolleranza +-1: una volta tagliati ne prendi 50 e li misuri.

• Se li trovi tutti e 50 di lunghezza 100,00 mm cosa pensi? Che sei abbastanza certo che tutti i 100 pezzi siano in tolleranza.
• Se ne trovi 50 di lunghezza 100,8 mm, 30 di lunghezza 100,9 mm e 20 di lunghezza 100,1 mm, cosa pensi? Che non puoi essere certo che negli altri 90 pezzi non ve ne sia almeno uno fuori tolleranza, anche se quelli controllati andavano bene.

E se non sei certo è meglio non spedire i pezzi al cliente (o accettarli da un fornitore)

Cosa è la distribuzione

Prometto di ritornare sull’argomento in un prossimo articolo, facendo anche intervenire un mio collega specializzato in questo tema, ma cercherò qui di darti alcune indicazione di base.

Prendi un tuo prodotto qualsiasi che abbia una caratteristica numerica da verificare (per esempio un foro), fai 50 misure e scrivile su un pezzo di carta. Otterrai un insieme di dati che ti potrebbe dire molto poco, quindi procedi così.

Ma prova ad inserire i dati in un foglio di Excel e rappresentare i dati misurati con il metodo degli istogrammi.

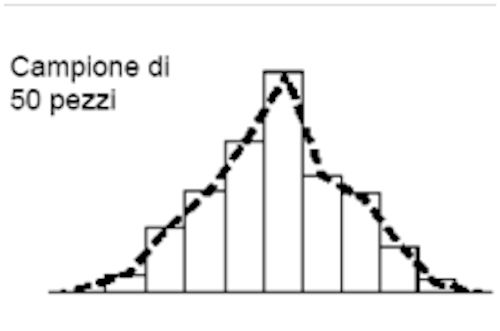
Nella figura sopra abbiamo rappresentato i dati misurati unendo le estremità degli istogrammi con una linea tratteggiata.
Se il campione ha una numerosità sufficientemente elevata, è probabile che la linea disegnata sarà una curva regolare che rappresenterà l’insieme della popolazione dei pezzi prodotti.

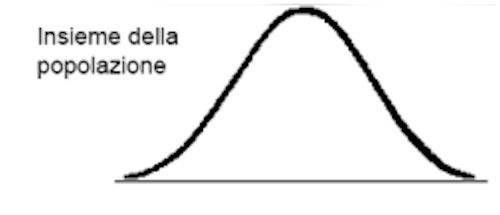
Il modello raffigurato sopra è chiamato distribuzione.

Un numero di campioni pari a 50 è un numero adatto per avere un’eccellente approssimazione (minimizzazione dell’errore).

Per il momento non approfondiamo l’argomento, ma sappi che la curva rappresentata sopra è definita curva di Gauss e rappresenta la distribuzione normale del prodotto analizzato.

Le proprietà fondamentali della curva sono:

• è simmetrica rispetto alla media (rappresentata normalmente da una X barrata)
• è asintotica (tende a 0 a +- infinito)

Questa curva è possibile disegnarla semplicemente disponendo di due parametri:

• media delle misure effettuate
• scarto tipo (normalmente indicato con S o con la lettera greca σ ).

La media è il valore a cui sono più prossime il maggior numero di misure effettuate, ed infatti coincide con il punto in cui la curva ha il suo massimo valore.

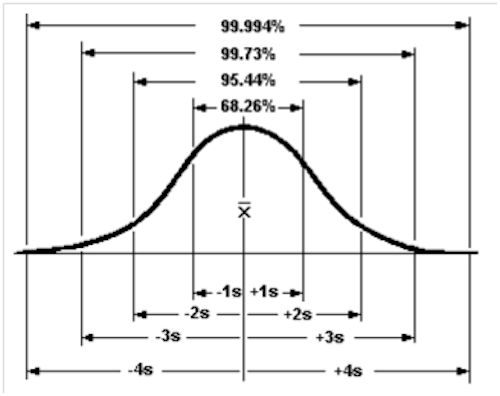
Facendo gli opportuni calcoli ottengo σ e quindi la curva che vedi sopra (che rappresenta l’intero lotto di produzione), grazie alla quale sarò in grado di sapere anche la percentuale di pezzi conformi e di non conformi.

Come mostrato nella figura sopra, nello spazio compreso tra +-4 σ sono compresi il 99,994% dei pezzi dell’intero lotto e quindi possiamo dire che, se sta nel campo di tolleranza, praticamente tutti i nostri pezzi sono conformi.

Spiego meglio ritornando all’esempio dei tubi:

se il campo di tolleranza va da 99,9 a 100,1 mm (2 decimi di millimetro) e la curva è larga 3 decimi di millimetro (e questo è possibile anche se tutti i campioni erano conformi), so già che nel mio lotto ci sono degli scarti.

Conclusioni

Oggi ho fatto solo un breve accenno all’utilità di studiare ed applicare la statistica di base per determinare quanto e quando controllare i prodotti che realizzi ed acquisti, avendo la certezza di non spedire prodotti di scarto ai clienti.

La statistica parla di probabilità e quindi, oltre a snellire i tuoi controlli riducendo tempi e costi, ti permette anche di fare previsioni utili alla tua azienda.

Se nella tua azienda non hai nessuno che abbia queste basi di statistica, o se i tuoi consulenti non ti hanno trasferito le competenze necessario, provvedi il prima possibile a colmare queste lacune.

Una volta imparate le tecniche ti meraviglierai di quanti problemi potrai risolvere, anche in altri ambiti, a costo zero e con risultati strabilianti, per esempio:

• ogni quanto tempo fare la manutenzione delle macchine?
• ogni quanto tempo fare le verifiche di conformità metrologica agli strumenti?
• che probabilità ho di consegnare il prodotto entro una certa data?

Posso continuare all’infinito, ma credo di essere stato abbastanza chiaro.

Ora tocca a te agire.

Semplifica la tua attività
contatta i consulenti MYMAX
Guarda le nuove proposte che ti ho riservato.